Опитайте Нашия Инструмент За Премахване На Проблемите

Изберете Операционната Система Изберете Програма За Проекция (По Желание)

Опишете Проблема Си

Обикновеното хармонично движение е изобретено от френския математик барон Жан Батист Жозеф Фурие през 1822 г. Едуин Армстронг (18 декември 1890 до 1 февруари 1954 г.) наблюдава трептения през 1992 г. в експериментите си и Александър Майснер (14 септември 1883 г. до 3 януари 1958 г.) осцилатори през март 1993 г. Терминът хармоник е латинска дума. Тази статия разглежда общ преглед на хармоничния осцилатор, който включва неговата дефиниция, тип и приложения.

Какво е хармоничен осцилатор?

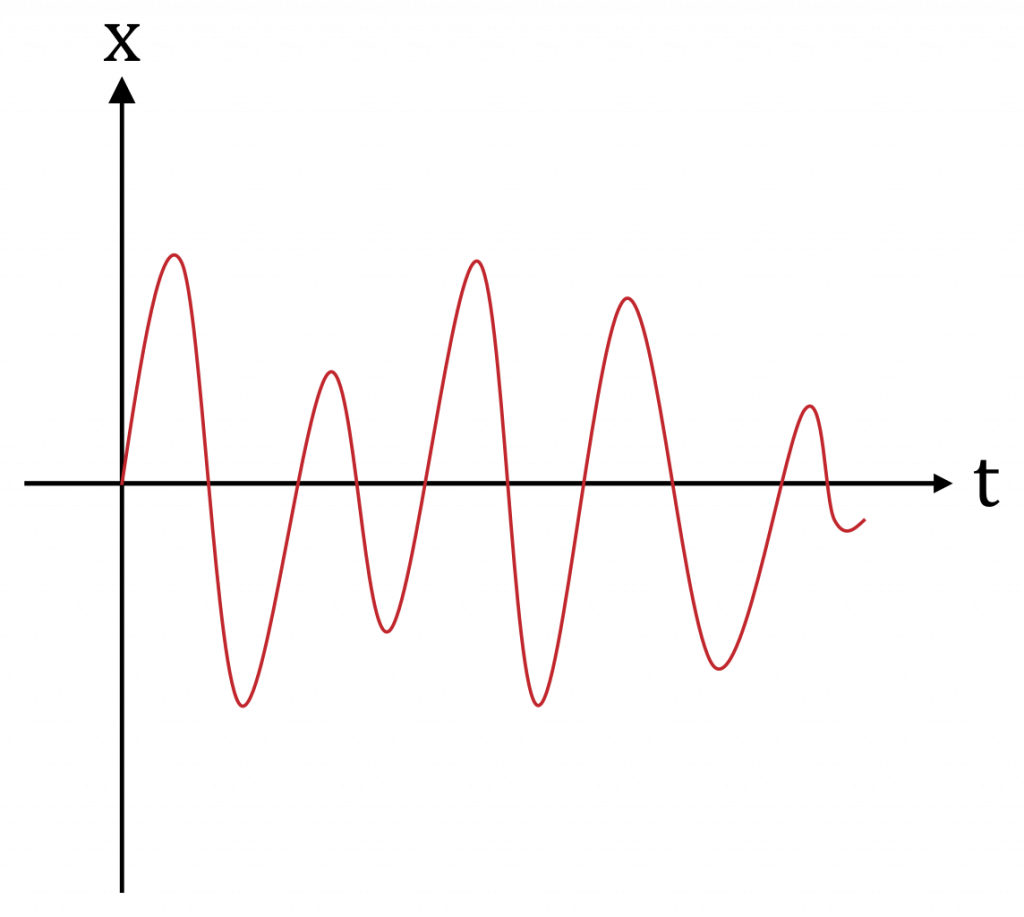
Хармоничният осцилатор се дефинира като движение, при което силата е право пропорционална на частицата от равновесната точка и произвежда изход в синусоидална форма на вълната. Силата, която причинява хармоника движение може да се изрази математически като

F = -Kx

Където,

F = Възстановяваща сила

K = пружинна константа

X = Разстояние от равновесието

блок-диаграма-на-хармоничен осцилатор

Има точка в хармоничното движение, в която системата се колебае и силата, която отново и отново привежда масата в същата точка, от която започва, силата се нарича възстановяваща сила, а точката се нарича точка на равновесие или средно положение. Този осцилатор е известен също като a линеен хармоничен осцилатор . Енергията тече от активна компоненти към пасивни компоненти в осцилатора.

Блокова диаграма

The блок-схема на хармоничния генератор състои се от усилвател и мрежа за обратна връзка. Усилвателят се използва за усилване на сигналите и че усилените сигнали се предават през мрежа за обратна връзка и генерира изхода. Където Vi е входното напрежение, Vo е изходното напрежение и Vf е напрежението на обратната връзка.

Пример

Меса на извор: Пружината осигурява възстановяваща сила, която ускорява масата и възстановителната сила се изразява като

F = ma

Където ‘m’ е масата, а a е ускорение.

“окабеляване 3 фаза към еднофазна ”

маса на пролетта

Пружината се състои от маса (m) и сила (F). Когато силата дърпа масата в точка x = 0 и зависи само от x - положението на масата и пружинната константа се представя с буква k.

Видове хармонични осцилатори

Видовете на този осцилатор включват основно следното.

Принудителен хармоничен осцилатор

Когато прилагаме външна сила към движението на системата, тогава се казва, че движението е принудителен хармоничен осцилатор.

Приглушен хармоничен осцилатор

Този осцилатор се дефинира като, когато прилагаме външна сила към системата, тогава движението на осцилатора намалява и се казва, че неговото движение е затихнало хармонично движение. Има три вида затихващи хармонични осцилатори

затихващи вълни

Над затихнал

Когато системата се движи бавно към точката на равновесие, тогава се казва, че е свръхзаглушен хармоничен осцилатор.

Под Damped

Когато системата се придвижва бързо към точката на равновесие, тогава се казва, че е свлачен хармоничен осцилатор.

Критично амортизиран

Когато системата се движи възможно най-бързо, без да се колебае около точката на равновесие, тогава се казва, че е свръхзаглушен хармоничен осцилатор.

Квантова

Изобретен е от Макс Борн, Вернер Хайзенберг и Волфганг Паули от „Университета в Гьотинген“. Думата квант е латинската дума, а значението на квант е малко количество енергия.

Нулева точка енергия

Енергията с нулева точка е известна още като енергия в основно състояние. Определя се, когато енергията в основно състояние винаги е по-голяма от нула и тази концепция е открита от Макс Планк в Германия и формулата, разработена през 1990 г.

Средна енергия на амортизирано просто хармонично осцилаторно уравнение

Има два вида енергии, те са кинетична енергия и потенциална енергия. Сборът от кинетична енергия и потенциална енергия е равен на общата енергия.

E = K + U ………………. Уравнение (1)

Където E = обща енергия

K = Кинетична енергия

U = потенциална енергия

Където k = k = 1/2 mv^две………… екв. (2)

U = 1/2 kx^две………… екв. (3)

колебания-цикъл- за-средни- стойности

Средните стойности на кинетичната и потенциалната енергия за цикъл на трептене са равни на

Където v^две= v^две(ДА СЕ^две-х^две) ……. еквалайзер (4)

Заместването на eq (4) в eq (2) и eq (3) ще получи

k = 1/2 m [w^две(ДА СЕ^две-х^две)]]

= 1/2 m [Aw cos (wt + ø₀)]]^две……. еквалайзер (5)

U = 1/2 kx^две

= 1/2 k [Грех (wt + ø₀)]]^две……. еквалайзер (6)

Замествайки eq (5) и eq (6) в eq (1) ще получите общата енергийна стойност

E = 1/2 m [w^две(ДА СЕ^две-х^две)] + 1/2 kx^две

= 1/2 m w^две-1/2 m w^двеДА СЕ^две+ 1/2 kx^две

= 1/2 m w^двеДА СЕ^две+1/2 х^две(K-mw^две) ……. еквалайзер (7)

Където mw^две= К , заместете тази стойност в eq (7)

E = 1/2 K A^две- 1/2 Kx^две+ 1/2 х^две= 1/2 K A^две

Обща енергия (E) = 1/2 K A^две

Средните енергии за един период от време се изразяват като

ДА СЕ_ср= U_ср= 1/2 (1/2 K A^две)

Функция на вълната на хармоничния осцилатор

Хамилтоновият оператор се изразява като сбор от кинетична енергия и потенциална енергия и се изразява като

ђ (Q) = T + V ……………… .eq (1)

Където ђ = хамитонов оператор

T = Кинетична енергия

V = Потенциална енергия

За да генерираме вълновата функция, трябва да знаем уравнението на Шрьодингер и уравнението се изразява като

-đ^две/ 2μ * d^двеѱ_υ(Q) / dQ^две+ 1 / 2KQ^двеѱ_υ(Q) = E_υѱ_υ(Q) …………. еквалайзер (2)

Където Q = Дължина на нормалната координата

Μ = Ефективна маса

K = постоянна сила

Граничните условия на уравнението на Шрьодингер са:

Ѱ (-∞) = ø

Ѱ (+ ∞) = 0

Можем да запишем и уравнението (2) като

д^двеѱ_υ(Q) / dQ^две+ 2μ / đ^две(Е_υ-K / 2 * Q^две) ѱ_υ(Q) = 0 ………… екв. (3)

Параметрите, използвани за решаване на уравнение, са

β = ђ / √μk ……… .. eq (4)

д^две/ dQ^две= 1 / β^двед^две/ dx^две………… .. eq (5)

Заместете eq (4) и eq (5) в eq (3), тогава диференциалното уравнение за този осцилатор става

д^двеѱ_υ(Q) / dx^две+ (2μb^двеЕ_υ/ đ^две- х^две) ѱ_υ(x) = 0 ……… .. eq (6)

Общият израз за степенни серии е

ΣC¬nx2 …………. еквалайзер (7)

Експоненциална функция се изразява като

exp (-x^две/ 2) ………… eq (8)

eq (7) се умножава с eq (8)

ѱυ (x) = ΣC¬nx2exp (-x2 / 2) …………… ..eq (9)

Ермитовите полиноми се получават чрез използване на уравнението по-долу

ђ_υ(x) = (-1)^υ* опит (x^две) d / dx^υ* exp (-x^две) …………… .. екв. (10)

Нормализиращата константа се изразява като

н_υ= (1/2^υυ! √Π)^1/2…………… .eq (11)

The просто решение за хармоничен осцилатор се изразява като

Ѱ_υ(x) = N_υЗ._υ(и) д^{-x2 / 2}……………… екв. (12)

Където N_υе константата на нормализиране

З. _υе отшелникът

е ^{-x2 / две}е Гаус

Уравнение (12) е вълновата функция на хармоничния генератор.

Тази таблица показва първите членове на полиноми на Ермит за състояния с най-ниска енергия

^υ	0	1	две	3
З._υ(Y)	1	2г	4г^две-две	8г³-12г

Вълновите функции на проста графика на хармоничен осцилатор за четири състояния с най-ниска енергия са показани на фигурите по-долу.

вълнови функции на хармоничен осцилатор

Вероятностните плътности на този осцилатор за четирите най-ниски енергийни състояния са показани на фигурите по-долу.

вероятностни плътности на вълнови форми

Приложения

Sреализира хармоничен осцилаторприложенията включват основно следното

Аудио и видео системи
Радио и други комуникационни устройства
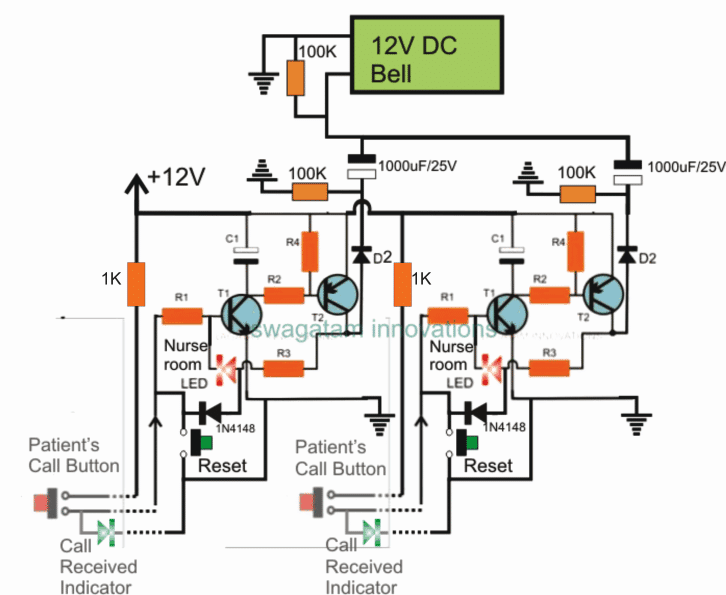
Инвертори , Аларми
Бръмчалки
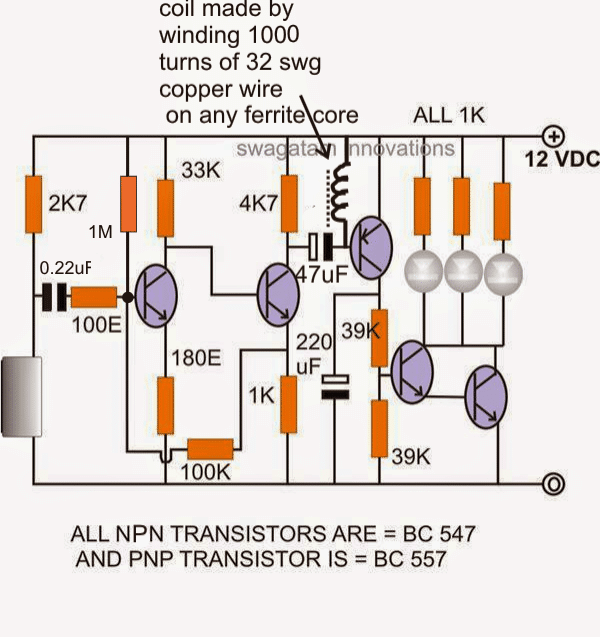
Декоративни светлини

Предимства

The предимства на хармоничния осцилатор са

Евтини
Високочестотно генериране
Висока ефективност
Евтини
Преносим
Икономичен

Примери

Примерът за този осцилатор включва следното.

Музикални инструменти
Обикновено махало
Масова пружинна система
Люлка
Движението на стрелките на часовника
Движението на колелата на автомобил, камион, автобуси и др

Това е един вид движение, което можем да наблюдаваме ежедневно. Хармонично осцилатор изведени са вълнови функции с помощта на Schrodinger и уравнения на хармоничния осцилатор. Ето един въпрос, какъв тип движение, изпълнявано от бънджи скокове?