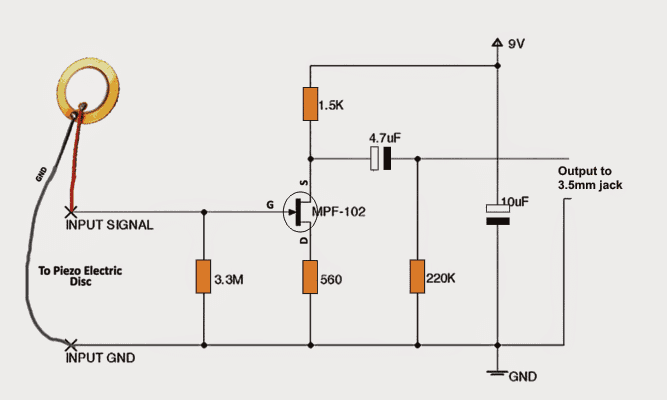
RLC верига е електрическа верига, която се състои от резистор, индуктор и кондензатор, те са представени с буквите R, L и C. Резонансните RLC вериги са свързани последователно и паралелно. Името RLC схема е получено от началната буква от компонентите на съпротивлението, индуктора и кондензатора. За текущата цел веригата образува хармоничен осцилатор. Използвайки LC верига то от резонира. Ако резисторът се увеличи, той разлага колебанията, които е известен като демпфиране. Трудно е да се намери известно съпротивление в реално време, дори след като резисторът не е идентифициран като компонент, той се решава от LC веригата.
Резонансни RLC вериги
Докато се занимава с резонанса, той е сложен компонент и има много несъответствия. Импедансът z и неговата верига се определят като
Z = R + JX
Където R е съпротивление, J е въображаема единица, а X е реактивно съпротивление.
Има импулс, подписан между R и JX. Въображаемата единица е външна съпротива. Съхранената енергия е компонентите на кондензатора и индуктор. Кондензаторите се съхраняват в електрическото поле, а индукторите се съхраняват в магнитудно поле.
С° С= 1 / jωc
= -J / ωc
СL= jωL
От уравнението Z = R + JK можем да определим реактансите като
х° С= -1 / ωc
хL =ωL
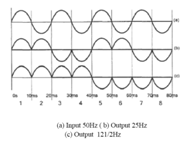
Абсолютната стойност на реактивното съпротивление на индуктора и кондензаторен заряд с честота, както е показано на фигурата по-долу.

Q фактор
Съкращението на Q се определя като качество и е известно и като фактор за качество. Факторът за качество описва недостатъчно затихналия резонатор. Ако резонансът с по-нисък демпфер се увеличи, коефициентът на качество намалява. Демпфирането на електрическата резонаторна верига генерира загуба на енергия в резистивните компоненти. Математическият израз на Q фактора се определя като
Q ( ω ) = максимална съхранена енергия / загуба на мощност
Коефициентът q зависи от честотата, която най-често се цитира за резонансната честота и максималната енергия, съхранявана в кондензатора и в индуктора, може да изчисли резонансната честота, която се съхранява в резонансната верига. Съответните уравнения са
Максимално съхранена енергия = LIдвеLrms= C VдвеCrms
ILrms се обозначават като средно ефективния ток през индуктора. Той е равен на общия RMS ток, образуващ се във веригата в последователната верига, а в паралелната верига не е равен. По същия начин, в VCrms е напрежение в кондензатора, което е показано в паралелната верига и е равно на средно ефективното захранващо напрежение, но в серията веригата е съгласувана от потенциален делител. По този начин последователната верига е проста за изчисляване на максималната енергия, съхранявана чрез индикатор и в паралелните вериги се разглежда чрез кондензатор.
Реалната мощност се дегенерира в резистора
P = VRrmsАзRrms= АздвеRrmsR = VдвеRrms/ R
Най-лесният начин да намерите серийната RLC верига
Въпрос:(С)ω0= ω0 АздвеrmsL / IдвеrmsR = ω0L / R
Паралелната верига трябва да вземе предвид напрежението
Въпрос:(P)ω0= ω0RCVдвеCrms/ VдвеCrms= ω0CR
Серия RLC верига
RLC серийната верига се състои от съпротивление, индуктор и кондензатор, които са свързани последователно в серийната RLC верига. Диаграмата по-долу показва серийната RLC схема. В тази верига кондензаторът и индукторът ще се комбинират помежду си и ще увеличат честотата. Ако можем да свържем Xcis отрицателно, така че е ясно, че XL + XC трябва да са равни на нула за тази специфична честота XL = -XCimpedance компоненти на въображаеми точно се отменят. При това честотно движение импедансът на веригата има ниска величина и фазов ъгъл от нула, той се нарича резонансна честота на веригата.

Серия RLC верига
хL+ X° С= 0
хL= - X° С= ω0L = 1 / ω0C = 1 / LC
ω0 =√1 / LCω0
= 2Π f 0
Произволна RLC схема
Можем да наблюдаваме резонансните ефекти, като разгледаме напрежението на резистивните компоненти към входното напрежение за пример, който можем да разгледаме за кондензатора.
VC/V = 1/1-ωдвеLC + j ωRC
За стойностите на R, L и C съотношението се нанася спрямо ъгловата честота и фигурата показва свойствата на усилване. Резонансна честота
VC / V- 1 / j ω0RC
VC / V- j ω0L / R
Виждаме, че тъй като това е положителна верига, общото количество разсейвана мощност е постоянно

Паралелна RLC схема
В паралелната RLC верига съпротивлението на компонента, индукторът и кондензаторът са свързани паралелно. Резонансната RLC верига е двойна последователна верига в ролята на обмен на напрежение и ток. Следователно веригата има текущо усилване, а не импеданс и усилването на напрежението е максимум при резонансната честота или е сведено до минимум. Общият импеданс на веригата е даден като

Паралелна RLC верига
= R ‖ ZL‖ С° С
= R / 1- JR (1 / X° С+ 1 / XL)
= R / 1+ JR (ωc - 1 / ωL)
Кога х° С = - хL Резонансните пикове идват отново и по този начин резонансната честота има същата връзка.
ω0 =√1 / LC
За да се изчисли усилването на тока, като се гледа токът във всеки от рамената, тогава усилването на кондензатора се дава като
i° С/ i = jωRC / 1+ jR (ωc - 1 / ωL)

Текущият коефициент на усилване е показан на фигурата, а резонансната честота е
i° С/ i = jRC
Приложения на резонансните RLC вериги
Резонансните RLC вериги имат много приложения като
- Осцилаторна верига , радиоприемници и телевизори се използват за настройка.
- Поредицата и RLC веригата включва главно обработка на сигнала и комуникационна система
- Серийната резонансна LC верига се използва за осигуряване на увеличение на напрежението
- При индукционно отопление се използват последователни и паралелни LC вериги
Тази статия дава информация за RLC верига, серия и паралели RLC вериги, Q фактор и приложения на резонансните RLC вериги. Надявам се дадената информация в статията да е полезна за даване на добра информация и разбиране на проекта. Освен това, ако имате някакви въпроси относно тази статия или на електрически и електронни проекти можете да коментирате в раздела по-долу. Ето въпрос за вас, в паралелна RLC схема, коя стойност винаги може да се използва като векторна референция?
Кредити за снимки: